Hi all!
I'm having some issues understanding where Casey derives the following form of the equation for reflecting the velocity vector about the wall vector: V - 2V·rr
I understand the alternative form intuitively: -V·rr + V·WW as it's easy for me to see how in this form the resultant vector is the combination of the 'r' and 'W' components of the velocity vector projected onto the r and W axes, respectively.
However I'm struggling to see how the other form is derived. Can anybody point me in the right direction?
Many thanks in advance!
- Jonny
I'm having some issues understanding where Casey derives the following form of the equation for reflecting the velocity vector about the wall vector: V - 2V·rr
I understand the alternative form intuitively: -V·rr + V·WW as it's easy for me to see how in this form the resultant vector is the combination of the 'r' and 'W' components of the velocity vector projected onto the r and W axes, respectively.
However I'm struggling to see how the other form is derived. Can anybody point me in the right direction?
Many thanks in advance!
- Jonny
Edited by panthalassadigital
on
For those equation I like to write them with parenthesis to make sure of the order of operation.
v - 2((v dot r) * r)
v is the vector that goes toward the impact point. Since it's a vector, if you consider the impact point as the origin, it's also the vector that went "inside the wall" from the origin. It also has "crossed" the normal so we already are on the "right side of the normal" (similar as not having to flip the x when you're aligned to the axis).
r is the normal from the wall. We represent it at the impact point going outside of the wall.
The sign of the dot product of v and r will be negative, meaning the two vectors go in opposite directions relative to the wall.
The absolute value of the dot product of v and r will tell us how much (scalar length) we are in the wall along the normal.
Consider v as a point (not a vector) with the origin at the impact point:
- we need to move the point in the direction of the normal (meaning parallel to the normal, not toward the normal);
- we need to know how much in that direction we need to move;
- it is given by the dot product between v and r (how much we are in the wall along the normal);
- but we know that the dot product is negative since the vectors go in opposite directions;
- so we need to negate it;
- if we move by r * -(v dot r) we will have a point on the wall (similar to the projection of the reflected point on the wall);
- if we do it again, we have the reflected point.
So we need to move by 2 * (r * -(v dot r)) which is the same as -2((v dot r) * r);
v - 2((v dot r) * r)
v is the vector that goes toward the impact point. Since it's a vector, if you consider the impact point as the origin, it's also the vector that went "inside the wall" from the origin. It also has "crossed" the normal so we already are on the "right side of the normal" (similar as not having to flip the x when you're aligned to the axis).
r is the normal from the wall. We represent it at the impact point going outside of the wall.
The sign of the dot product of v and r will be negative, meaning the two vectors go in opposite directions relative to the wall.
The absolute value of the dot product of v and r will tell us how much (scalar length) we are in the wall along the normal.
Consider v as a point (not a vector) with the origin at the impact point:
- we need to move the point in the direction of the normal (meaning parallel to the normal, not toward the normal);
- we need to know how much in that direction we need to move;
- it is given by the dot product between v and r (how much we are in the wall along the normal);
- but we know that the dot product is negative since the vectors go in opposite directions;
- so we need to negate it;
- if we move by r * -(v dot r) we will have a point on the wall (similar to the projection of the reflected point on the wall);
- if we do it again, we have the reflected point.
So we need to move by 2 * (r * -(v dot r)) which is the same as -2((v dot r) * r);
Edited by Simon Anciaux
on
Reason: typo
mrmixer
- if we move by r * -(v dot r) we will have a point on the wall (similar to the projection of the reflected point on the wall);
- if we do it again, we have the reflected point.
I guess I'm still kinda confused about this aspect of what you said. I'm happy to accept that this is true, but I'm confused as to why this is true. Maybe this is more of a general question that requires some additional maths educatio on my part?
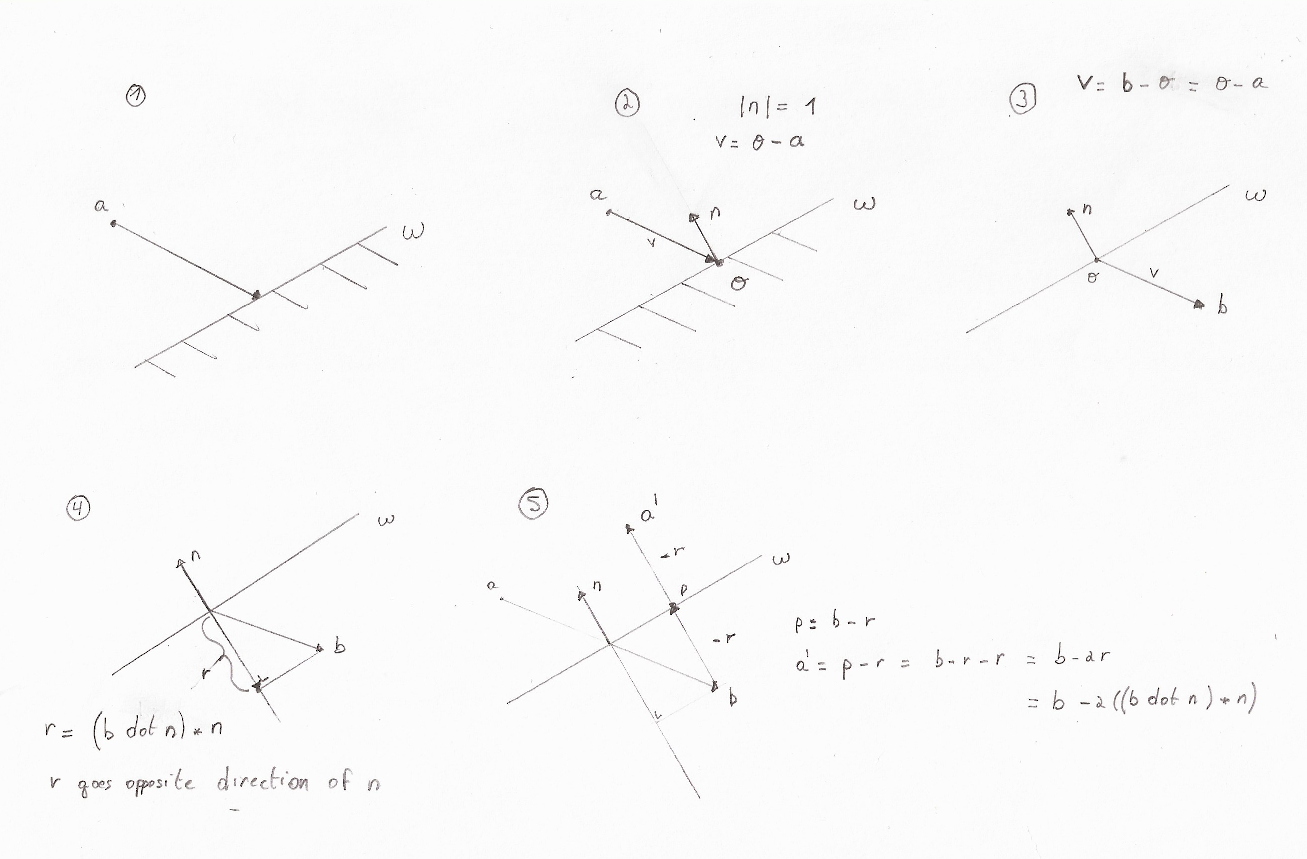
Maybe those drawings would help ? (Sorry I didn't keep the same vector names)

Edited by Simon Anciaux
on
Reason: note
Simon, thank you so much for the drawing - that explanation was perfect. I really appreciate it :)